Pharmacy Calculations: Molecular Weights and Moles

Introduction Molecular Weights and Moles

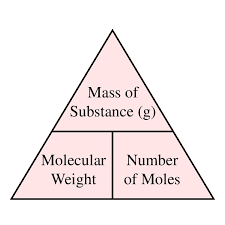
Molecular Weights and Moles : Understanding molecular weights and moles is essential in pharmacy calculations. These concepts are fundamental to determining dosages, concentrations, and ingredient proportions in pharmaceutical formulations. While these ideas are not inherently difficult, they are crucial for accurate calculations. Instead of dealing with everyday units like kilograms or pounds, pharmacy professionals work with molecular weights and moles. Gaining a deep understanding of these terms will make pharmacy calculations much more manageable. This guide will break down these concepts and demonstrate how to use them effectively in pharmacy practice. Below are several examples that illustrate step-by-step solutions for common problems encountered in pharmaceutical calculations.

Section 1: Examples of Molecular Weight and Moles Calculations

Example No.	Problem	Step 1: Formula / Information	Step 2: Calculation	Answer
Example 1	Sodium Ion Content in Sodium Chloride Tablet	Molecular weight of NaCl = 23 (Na) + 35.5 (Cl) = 58.5	Sodium ion fraction = 23/58.5	235.9mg of sodium ions in a 600mg tablet of sodium chloride
Example 2	Lithium Content in Lithium Carbonate Tablet	Molecular weight of Li₂CO₃ = 2(7) + 12 + 3(16) = 74	Lithium fraction = 14/74 × 100	18.92% of the tablet is lithium
Example 3	Equivalent Iron Content in Ferrous Sulphate and Ferrous Gluconate	Molecular weight of FeSO₄ = 56 (Fe) + 32 (S) + 64 (O₄) = 152	Iron fraction in FeSO₄ = 56/152 = 36.84%	73.68mg of iron in 200mg of ferrous sulphate. Equivalent weight of ferrous gluconate = 634.2mg
Example 4	Adrenaline Injection Content	Molecular weight of adrenaline = 183, adrenaline acid tartrate = 333	Proportional calculation: 100 (adrenaline)/183 = z (adrenaline acid tartrate)/333	182 micrograms of adrenaline acid tartrate in each milliliter of injection
Example 5	Estimating Molecular Weights of Quinine Salts	Molecular weight of quinine anhydrous = 324, quinine bisulphate = 169, quinine dihydrochloride = 122	Proportional calculation for bisulphate and dihydrochloride	Molecular weight of quinine bisulphate = 548, quinine dihydrochloride = 395
Example 6	Codeine Phosphate Sesquihydrate vs. Hemihydrate	Molecular weight of hemihydrate = 406, sesquihydrate = 424	Proportional calculation: 30 (hemihydrate)/406 = z (sesquihydrate)/424	31.33mg of codeine phosphate sesquihydrate is equivalent to 30mg of codeine phosphate hemihydrate
Example 7	Moles of Chloride Ion in Calcium Chloride	Molecular weight of CaCl₂ = 110	Moles of CaCl₂ = 0.5g/110 = 0.0045 moles; Chloride ions = 0.0045 × 2 = 0.009 moles	0.009 moles of chloride ions in 500mg of calcium chloride
Example 8	Moles of Water in Hydrated Calcium Chloride	Molecular weight of CaCl₂·6H₂O = 219	Moles of hydrated calcium chloride = 0.5g/219 = 0.0023 moles; Water moles = 0.0023 × 6 = 0.0137 moles	0.0137 moles (13.7 millimoles) of water in 500mg of CaCl₂·6H₂O
Example 9	Moles of Solute in 20mL of a 1 mol/L Solution	1 mol/L solution means 1 mole in 1 liter	Moles = (1 × 20) / 1000 = 0.02 moles	0.02 moles of solute in 20mL of a 1 mol/L solution
Example 10	NaCl Needed for 25mL of 0.5 M Solution	Molecular weight of NaCl = 58.5	Moles of NaCl = (0.5 × 25) / 1000 = 0.0125 moles; Amount of NaCl = 0.0125 × 58.5 = 0.73125g	0.73125g of NaCl is required for 25mL of 0.5 M solution
Example 11	Moles of Sodium and Chloride in Sodium Chloride Infusion BP	Sodium chloride infusion BP contains 0.9% NaCl	0.9% NaCl = 9g in 1L; Moles of NaCl = 9g/58.5g/mol = 0.154 moles	154 millimoles of both sodium and chloride ions in 1L of sodium chloride infusion BP
Example 12	Sodium Fluoride for 250mL of Mouthwash	Molecular weight of NaF = 42	Moles of NaF = 0.012 × 250 / 1000 = 0.003 moles; Amount of NaF = 0.003 × 42 = 0.126g	0.126g of sodium fluoride needed for 250mL of mouthwash

Section 2: Introduction to Moles

A mole is the SI unit used to express amounts of a substance. It represents a quantity equal to Avogadro’s number (6.022×10236.022 \times 10^{23}6.022×1023) of entities, such as atoms, molecules, or ions. The concept of a mole allows pharmacists to work with manageable quantities in solution preparation and drug formulations.

Understanding Moles and Molecular Weights in Pharmacy

In pharmaceutical calculations, moles refer to the quantity of a substance, expressed in terms of the number of molecules, atoms, or ions present. The molecular weight (also called molecular mass) of a substance is the sum of the atomic weights of the atoms in the molecule, typically expressed in grams per mole (g/mol).

When preparing pharmaceutical solutions, the concept of molarity plays an essential role. Molarity refers to the concentration of a solute in a solution, measured in moles of solute per liter of solution (mol/L). A 1 M solution contains 1 mole of solute dissolved in 1 liter of solution. In the examples provided earlier, many of the calculations required us to understand the relationship between moles, molecular weight, and the final concentration or quantity of a substance in a solution or tablet.

Application in Pharmaceutical Formulation

For instance, in Example 4, we calculated the amount of adrenaline acid tartrate required to deliver 100 micrograms of adrenaline. Adrenaline acid tartrate has a molecular weight of 333, while adrenaline itself has a molecular weight of 183. By using the proportion between the molecular weights, we were able to determine the exact amount of adrenaline acid tartrate needed to provide the correct dosage of adrenaline.

This kind of calculation is crucial in drug formulation to ensure that each dose contains the appropriate amount of active pharmaceutical ingredient (API). Pharmacists need to be precise when working with drugs like adrenaline, where the exact concentration in a given volume of injection can impact the patient’s treatment outcomes. Understanding molecular weights and moles ensures that medication dosing is consistent and accurate, minimizing the risk of over- or under-dosing.

More Complex Examples

In Example 6, we explored how to convert the amount of codeine phosphate hemihydrate to its sesquihydrate form. This involved using proportional sets to determine that 31.33mg of codeine phosphate sesquihydrate would be required to match the 30mg of codeine phosphate hemihydrate in terms of the actual codeine content. This is particularly relevant when patients are prescribed medications in various forms, such as different hydrated or salt forms of a compound. These forms can have different molecular weights, so conversions between them ensure accurate dosing.

Similarly, in Example 7, we calculated the number of moles of chloride ions in a given amount of calcium chloride. We learned that 500mg of calcium chloride contained 4.5 millimoles of calcium chloride, and because calcium chloride dissociates into two chloride ions per calcium ion, the number of chloride ions present would be double that—9 millimoles. This type of calculation is essential for preparing intravenous (IV) solutions where the correct ion balance is required for patient safety. Miscalculations could lead to electrolyte imbalances, which could cause serious health issues.

Practical Use of Moles in Dosage Calculation

Another example that demonstrates the importance of mole calculations in pharmacy is Example 10, where we calculated how much NaCl (sodium chloride) is required to make a 0.5 M solution. Sodium chloride is commonly used in saline solutions, and understanding the required amount of solute based on molarity is a standard practice in pharmacy. The calculation led to the conclusion that 0.73125g of NaCl is required to make 25mL of a 0.5 molar solution. This would be useful in preparing saline solutions for various medical purposes, from IV fluids to wound care.

Additionally, Example 12 further emphasizes the significance of mole calculations when preparing medications like mouthwash. We found that 0.126g of sodium fluoride is needed to make 250mL of mouthwash containing 0.012 mol/L of sodium fluoride. This example illustrates how knowledge of moles and molecular weight is key in accurately formulating consumer healthcare products, ensuring the proper dosage of active ingredients.

Conclusion and Practical Takeaways

In conclusion, pharmacy calculations based on molecular weights and moles are vital for the accurate preparation and administration of pharmaceutical products. By understanding the relationship between the molecular weight of a substance and the number of moles, pharmacists can confidently calculate the correct amounts of drugs or chemicals needed in different formulations, ensuring that patients receive the right dosages. Whether calculating the amount of active ingredient in a tablet, the concentration of a solution, or the proper amount of a hydrated compound, these foundational calculations are crucial to patient safety and effective drug delivery.

As you continue to practice and work through examples, keep these key concepts in mind:

Molecular weight is a critical starting point for all calculations in pharmacy.
Moles provide the bridge between weight and the number of molecules or ions.
Using proportions helps simplify complex calculations and conversions between different forms of compounds (e.g., salts or hydrates).
Regular practice with these types of calculations ensures proficiency in pharmaceutical preparations and prevents errors.

Through consistent application and understanding, pharmacy students and professionals can excel in dosage calculations, ultimately ensuring that medications are formulated and administered safely to patients

Conclusion

Mastering the calculation of molecular weights and moles is essential for pharmaceutical professionals. These calculations are central to determining the correct dosages, concentrations, and ingredient amounts for drug formulations. By understanding the molecular composition of substances and how they relate to their physical properties, such as moles, you can confidently perform these critical calculations.

Be sure to practice regularly, as repetition is key to mastery. The more familiar you are with concepts like molecular weights, moles, and proportional calculations, the easier pharmacy exams and real-world applications will become.

Pharmacy Calculations: Molecular Weights and Moles 2025